Optical pumping (OP) in open level systems can lead to curios effects on lineshapes at laser intensities well below the saturation limit. If a two-level system interacts with near-resonant photons, the ground state g is radiatively broadened, with the width 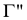given by [1]

,

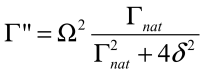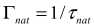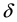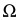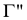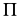where is the natural width of the excited state e, is the detuning from the line centre, and is the Rabi frequency. The width is equal with the rate of the spontaneously emitted photons. In the case of an open level system, only a fraction of the spontaneous transitions returns population to the initial state g, while the fraction 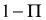leaves the (g,e)-system. The rate of such pumping is obviously 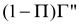, and the corresponding pumping time is

.

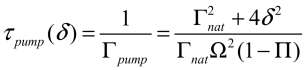Depletion of the system will be remarkable for Rabi frequencies, which ensure that pumping time is shorter than transit time 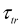of atoms through the laser field. The critical value of Rabi frequency is given by 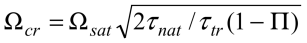, where Ω_sat is the saturation Rabi frequency [2]. In terms of laser intensities it can be rewritten as

.

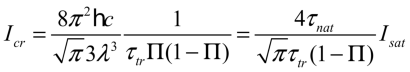The above equation implies that the critical laser intensity I_cr has a minimum when 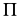=0.5. Hence, the nonlinear effects are more pronounced for transitions with branching coefficients 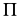close to 0.5.

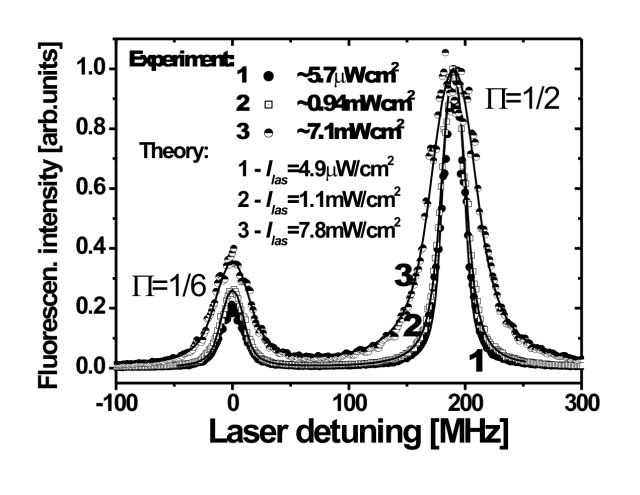
Broadening by optical pumping can be demonstrated, for example, by laser excitation of the 3s_1/2(F"=1) → 3p_1/2(F'=1,2) transition in a supersonic beam of Na atoms, under the conditions when transit time τ_tr=2700 ns is much larger than the natural lifetime τ_nat=16.4 ns of the 3p state. In that case, I_cr << I_sat, therefore broadening and saturation of HF components in the excitation spectrum should occur at laser intensities well below the saturation intensity. This is confirmed by the experiment (see Fig. 1). Significant broadening of spectral lines in the excitation spectrum is observed well below the saturation intensities (I_sat = 37.4 and 12.5 mW/cm² for lhs and rhs components, respectively).       The studies also showed that that presence of dark (i.e., not laser- coupled) Zeeeman sublevels in the lower state results in effective branching coefficients which vary with laser intensity and differ from those implied by the sum rules, and this can lead to peculiar changes in peak ratios of hyperfine components of the spectra. These results are published in [3]. 

Fig. 1.
Excitation spectra of the 3s_1/2, F′′ = 1 → 3p_1/2, F′ = 1, 2 transitions in Na. Residual Doppler width due to finite collimation angle is Δν_D=11.2 MHz. The expected peak ratio is 1:5. Saturation intensities of the lhs and rhs components are 37.4 and 12.5 mW/cm2, respectively.  

References

[1] C. Cohen-Tannoudji, Rev. Mod. Phys. 70, 707 (1998).

[2] H.J. Metcalf and P. van der Straten, Laser Cooling and Trapping (Springer, 1999).

[3] I. Sydoryk, N. N. Bezuglov, I. I. Beterov, K. Miculis, E. Saks, A. Janovs, P. Spels, and A. Ekers, Phys. Rev. A (2008) in print. 

---