I. Introduction.
Recent advances in quantum optics have led to the discovery of many novel and intriguing phenomena such as electromagnetically induced transparency (EIT) [1], narrowing of spectral lines [2], and lasing without inversion (LWI) [3]. The underlying effect in all of them is the destructive quantum interference between different excitation pathways leading to reduction or full cancellation of transition probabilities. The first coherent interference experiment showing cancellation of absorption was performed by Fano [4] and subsequently led the idea of coherent population trapping (CPT) [5]. In a typical lambda scheme, a certain ratio of the applied field strengths leads to the creation of a ‘dark’ state.
Taichenachev et al. [6] have obtained analytical expressions for dark resonance line shapes, where the full atomic structure, including magnetic and hyperfine levels, is included. Hioe and Carroll [7] investigated the behaviour of a multilevel quantum system interacting with a strong laser field and demonstrated the existence of different invariants (including CPT) depending on the number of levels N. Experimental observation of CPT in 87Rb vapor cell was reported by Zhu et al. [8], where multilevel dark states were created between two or three out of five degenerate magnetic sublevels in one of the ground state hyperfine levels.
The above phenomena are related to the Autler-Townes (AT) effect [9]. While extensively studied in atoms [10], experiments in molecular systems are still relatively few [11]. The AT effect has a potential for new applications to molecular spectroscopy, like measurement of the transition dipole moments [11a-d] and lifetimes of highly excited molecular states using cw laser fields [11d], and all-optical alignment of non-polar molecules [11c].
McClean and Swain [12] discussed that the three-level resonant model of Feneuille and Schweinhofer [13] can not adequately describe the AT splitting experiment of Pique and Pinard [10a] in Na atoms. They investigated the effect of non-resonant neighboring hyperfine levels as well as the role of magnetic sublevel degeneracy and concluded that both can significantly modify the population of the upper level, especially at high laser intensities.
The present study is focused on effects of hyperfine structure on the AT effect. We consider ladder systems of hyperfine levels F in Na atoms and Na2 molecules (see Fig. 1), each of which is 2F+1-fold degenerate over the magnetic number MF. Of special concern is determination and interpretation of the conditions under which the hyperfine interaction becomes negligible. An intuitive assumption would be that the coupling of hyperfine components by the laser field depends on the hyperfine and magnetic quantum numbers, which would lead to a different AT splittings for different MF components. The calculations show, however, that systems with large and small hyperfine splittings actually respond differently to coupling by strong laser fields.
II. Large HF splitting
II.A. Excitation scheme in Na atoms
Large HF splittings are usually observed in low-lying energy levels of atoms. We consider a ladder scheme of three atomic states in Na, where each state has a well resolved hyperfine structure (Fig. 1a). A weak probe laser P excites the atoms from the ground state |g> (3S1/2, Fg =1, 2) to the intermediate state |e> (3P1/2 state, Fe =1, 2), which is further coupled by a strong laser field S to the final state |f> (5S1/2, Ff =1, 2). Unless specified otherwise, the laser linewidth is assumed to be 1MHz. Both laser fields are linearly polarised, which implies the selection rule DMF = 0 for laser-driven transitions. The transition dipole matrix element between two MF magnetic sublevels of two hyperfine F states can be evaluated as [14]
(1)
where 
is the reduced matrix element, and () and {} brackets represent the 3j and 6j symbols, respectively. Since the Rabi frequency of the strong coupling field is proportional to (1), the F and MF dependence transfers to the splitting of the AT doublet. Therefore, we expect the excitation spectrum of levels |e> and |f> to consist of a number of AT split peaks, associated with each hyperfine and magnetic sublevel components.
II.B. Theoretical model
The optical Bloch equations (OBEs) for the density matrix are given by
, (2)
where the total Hamiltonian
of the atom-laser system includes the unperturbed atomic Hamiltonian as well as the dipole interaction operator 
. The relaxation term 
accounts for relaxation due to spontaneous emission and transit relaxation of the molecules through the laser beam. Equation (2) results in a system of OBEs for Zeeman coherences
and optical coherences
. The solution of this system yields populations of levels |g>, |e>, and |f>. For a full description of the model see [15].
II.C. Numerical Results for Atoms
We perform numerical simulations based on the OBEs model including the interaction of both laser fields with all the hyperfine levels in the system. Doppler broadening is not taken into account. Figure 2 shows the |f> state population as a function of probe field detuning for four different values of the coupling field Rabi frequency. At low intensity of the coupling field (Fig. 2a) the spectrum consists of two pairs of peaks which correspond to two-photon (one from the probe filed and one from the coupling field) excitation from the two ground state hyperfine levels to the two hyperfine components of level |f>. With the increase of the coupling field Rabi frequency, a separation of the Zeeman components MF is seen (Figs. 2b and 2c) until their full resolution at WS=2GHz (Fig. 2d). In the latter case the coupling field Rabi frequency exceeds the hyperfine splittings of both the 3P1/2 state (DE F=1,F=2=188.88 MHz) and the 5S1/2 state (DE F=1,F=2=156 MHz) by more than ten times. The number of hyperfine components in the AT spectrum is in accordance with the number of possible couplings of MF sublevels in levels |g>, |e> and |f>, which are subject to the selection rule DMF = 0 and an additional restriction of the MF' =0 → MF = 0 transition if F' = F.
It is instructive to see what would happen in the case of smaller HF splittings. For the sake of simplicity we shall consider only the transition Fg=1→|e>→|f>. Figure 3 shows the variation of the excitation spectrum of level |f> at WS=2GHz as the hyperfine constant Ahfs of level |f> is reduced. The spectrum is initially split in two triplets at the original Ahfs = 78MHz (Fig. 3a). When Ahfs is reduced by a factor of two, the outermost components off each triplet remain at the same positions, while the middle ones are shifted towards the respective rhs outermost peaks (Fig. 3b). When Ahfs is reduced by a factor of 10, the middle peaks is shifted even more and cannot be resolved for the rhs peaks.
The above results are consistent with the reuslts obtained using a much simpler treatment of laser-atom system based on solving the Shrödinger’s equation, which yields the time evolution of the probability amplitudes in the atomic wavefunction. Comparison with the simulations obtained by both approaches (Fig.4) shows the same energy positions of the MF Zeeman sublevels under the action of a strong laser field but different widths and intensities of the AT peaks, since no cascading due to spontaneous emission is included in Shrödinger’s equation.
III. Small HF splitting
III.A. Excitation Scheme in Molecules
Small HF splittings of energy levels are characteristic to molecules. We consider a ladder of three rovibronic levels in Na2 with hyperfine structure (Fig. 1b), where state |g> is the X1S+g (J=1) state, state |e> is the A1S+u (J=0) state and 51S+g (J=1) represents the final state |f>. The hyperfine splittings are of an order of 10-1÷102 kHz, which is well bellow the natural widths of levels |e> and |f>.
The nucleus of the sodium 23Na atom has a spin of 3/2, which leads to a total nuclear spin of I =3, 2, 1, or 0 for the sodium molecule. Since the atomic nucleus obeys the Fermi statistics, the total molecular wave function has to be anti-symmetric, e.g. symmetric rotational levels must have anti-symmetric nuclear spin functions, and vice versa. This leads to certain restrictions on the values of I for the chosen rotational levels. For the X1S+g (J=1) and 51S+g (J=1) states the possible values of the total nuclear spin and hyperfine number are I=0, F=2, 1, 0 or I=3, F=4, 3, 2. For the A1S+u (J=0) state I=0, F=1 or I=3, F=3. Since DI=0 selection rule holds for transitions between hyperfine levels, we consider only excitations between levels with I=3 for simplicity.
III.B. Numerical Results for Molecules
The final state population calculated with OBEs model as a function of the probe laser detuning for a value WS=500 MHz is given in Fig.5. Figures 5a-c show the full resolution of the magnetic sublevels MF when only one hyperfine level Ff =2, 3 or 4 in the final state is considered. However, the inclusion of more than one hyperfine level in the final state leads to a complete loss of the MF structure (Fig.5d); the states behave as J levels with MJ sublevels with no hyperfine structure. Similar results are obtained if narrow laser linewidths (1 Hz) and long lifetimes of excited states (t = 100 ms) are used.
Solving the Shrödinger’s equation for the molecular case shows that if the Rabi frequencies are smaller than the HF splittings, then the HF structure is well resolved in the excitation spectrum of the upper level (Fig. 6a). If the Rabi frequency of the strong coupling field is increased, some of the HF components lose intensity (Fig. 6b), while at large intensities (Fig. 6c) only the outer ones remain and the spectrum looks basically the same as Fig. 5d would be in the case of narrow laser linewidths, long lifetimes of excited states and small Rabi frequency of the probe field (100 Hz).
The latter is an interesting observation which contrasts with the behaviour of dressed levels in the case of large HF splittings. When the HF splitting is large, then increased Rabi frequency of the strong coupling field leads to a better resolution of the multitude of dressed states built of different HF levels. When the HF splitting is small, then increased Rabi frequency of the strong coupling field leads to a complete disappearance of the HF structure.
IV. Creation of Multiple Dark States
In order to understand the above effects, we applied the Shrödinger’s equation method for the model excitation scheme shown in Fig. 7, where the final state consists of six closely spaced levels separated by D = 100 KHz. As can be seen from Figs.8 a-d, the increase of the coupling field strength WS compared to values larger than the
separation D between the final states leads to a gradual decrease (Figs. 8a-c) and eventually vanishing (Fig. 8d) of the intensity of all AT peaks except the two outer ones.
The above effect can be interpreted by examining the dressed-states approach. Consider the situation when a molecular quantum state 
is coupled with a system of quantum states 
by the laser field 
as it is depicted on Fig 9a. The corresponding Rabi frequency 
may have arbitrary values. Our aim is to find a set of dressed states. In the rotating wave approximation the coupling diagram can de depicted as in Fig. 9b. The total Hamiltonian 
of such a system has the form
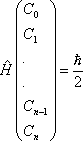
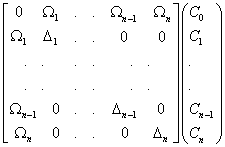, (3)
which is in the basis of the bare states 
(
). The corresponding solution 
of the Shrödinger’s equation may be expressed via the coefficients 
in the following way:
(4)
The Hamiltonian 
corresponds to a free molecule and determines the bare state energies 
(
). The value 
for the low-lying state 
is chosen as zero. The values of 
correspond to the diagonal elements and given by laser detunings from resonance frequencies 
of the corresponding optical transitions. The Rabi frequencies 
give nondiagonal matrix elements and are determined with the coupling term 
of the Hamiltonian.
In order to diagonalize the coupling part, we shall first find all solutions 
of the equation
(5)
Importantly, the wave function 
does not contain . Obviously, is not involved in the laser-system interaction (see Fig. 9c); hence, it is a dark state. The coefficients 
obey a simple relation 
. It is convenient to rewrite the latter as an orthogonal condition
; 
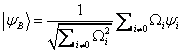, (6)
between and newly introduced some wave function 
. Straightforward calculation yields
, (7)
i.e. the function appears, in contrast to all , to be strongly coupled with the low-lying state with the effective Rabi frequency 
; , thus, may be considered as an analogue of a bright state.
Equation (6) implies that the subspace 
, which includes the dark states, is orthogonal to the one-dimensional subspace containing the single bright state. In the other words, the dimension of is n-1, i.e., there are n-1 mutually orthogonal dark states. The corresponding new diagram for the coupling matrix is depicted in Fig. 9c. If the interaction is strong, i.e., if the separation between the bare state energies are negligible compared to the effective Rabi frequency
, (8)
then the subspace is not excited by the laser field. Only the bright state is involved in the interaction with the low-lying states, which results in the formation of two dressed states 
with energies 
:
; 
; 
.
In experiment, the situation depicted on Fig. 9c corresponds to the excitation of only two levels , i.e., only one doublet would appear in the excitation spectrum.
V. Conclusion
The simulations of Autler-Townes spectra for molecules with small hyperfine splittings of energy levels show that when a strong coupling field is used, the hyperfine structure cannot be resolved (Fig. 5d, Fig. 6c). The dressed state analysis leads to a conclusion that resolution of MF Zeeman sublevels is not possible because of the formation of multiple dark states in a multilevel system coupled by laser field with Rabi frequency much larger than the level separation. It is, however, not yet quite clear why the MF resolution is not lost in the atomic hyperfine level system, when the coupling Rabi frequency is much larger than the HF level separations (Fig. 2d). Further investigation of AT effect in level systems with hyperfine structure are in progress and will be reported elsewhere.
This work was funded by the EU FP6 TOK project LAMOL, Latvian Science Council, and UL project Y2-ZP-114-100. I.I.R. and N.N.B. acknowledge support from RFBR grants No. 08-02-00220 and No. 09-02-92428.
Fig. 1: Excitation schemes in Na (frame (a)) and Na2 (frame (b)).
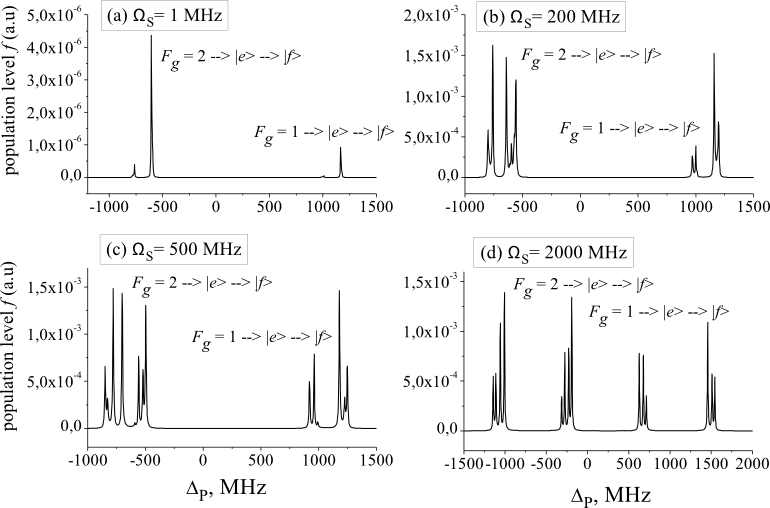
Fig. 2: Population of level |f> vs probe field detuning for different S field Rabi frequencies. Simulations are performed using parameters Wp=1 MHz, transit relaxation of 1 MHz, laser linewidth of 1 MHz for both laser fields, and lifetimes of the 3P1/2 and 5S1/2 states of 16.35 ns and 77.6 ns, respectively.
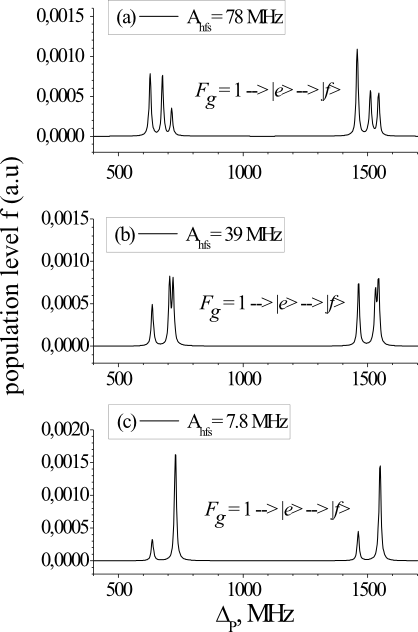
Fig. 3: The Fg=1→|e>→|f> component of the excitation spectrum in Fig. 2d for different values of Ahfs. Other simulation parameters are equal to those used in Fig. 2.
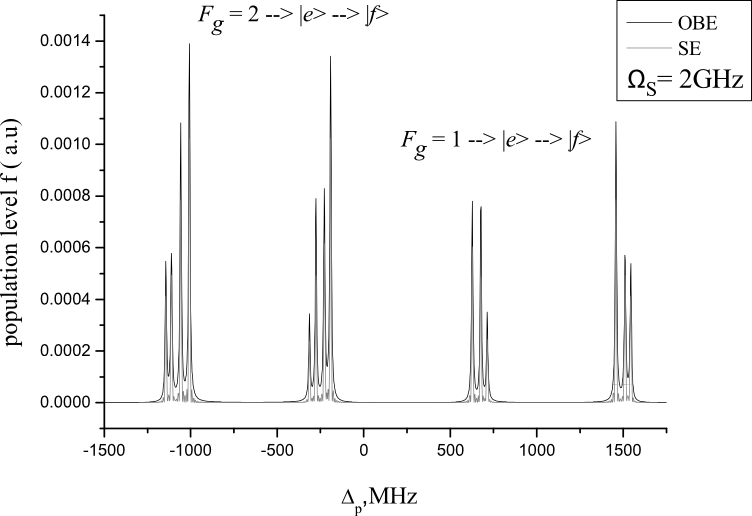
Fig. 4: Comparison of AT spectra obtained by the solution of OBEs and Schrödinger's equation. Simulation parameters are equal to those used for Fig. 2d.
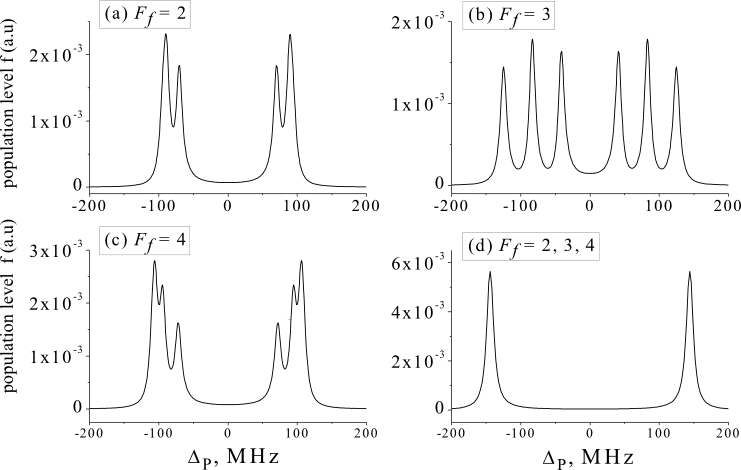
Fig. 5: Population of level |f> vs probe field detuning calculated for each hyperfine component separately (frames (a), (b), and (c)) and for all components simultaneously (frame (d)). The simulations were performed with WS=500 MHz, Wp=1 MHz, transit relaxation of 10 kHz, linewidths of both laser fields of 10 kHz, and lifetimes of the A1S+u and 51S+g states of 12.45 ns and 40 ns, respectively.
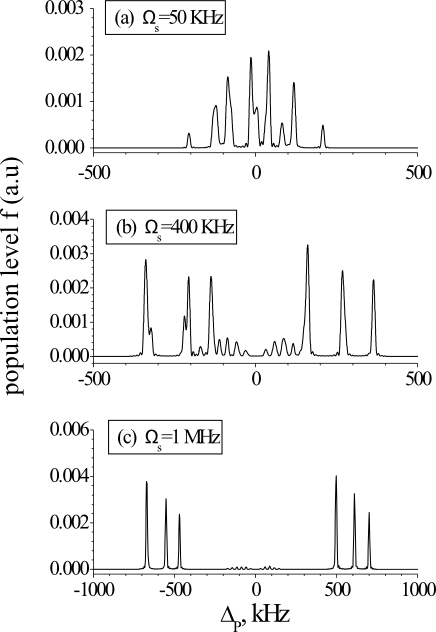
Fig. 6: Population of level |f> vs probe field detuning using Schrödinger's equation for different Rabi frequencies of coupling field: (a) WS = 50KHz; (b) WS = 400KHz; (c) WS = 1MHz. The simulations were performed with Wp = 1KHz and Ahfs=29KHz.
Fig. 7: Model system for state |f> consisting of six closely spaced levels |1>, …, |6> separated by D = 100 KHz and coupled by a strong laser filed ES to level |e>, while levels |g> and |e> are coupled by a weak probe field EP.
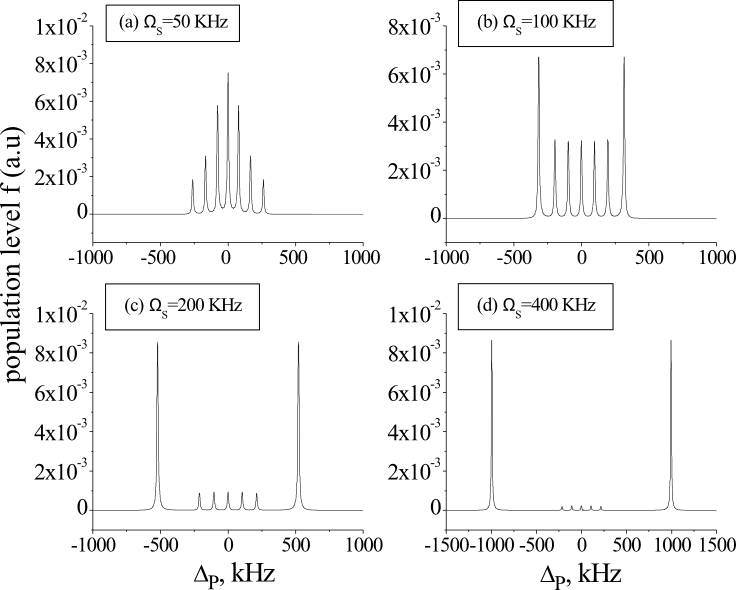
Fig. 8: Population of level |f> vs probe field detuning for different Rabi frequencies of coupling field: (a) WS = 50KHz; (b) WS = 100KHz; (c) WS = 200KHz; (d) WS = 400KHz. The simulations were performed with Wp = 1KHz, D=100KHz, and the decay rates of levels |e> and |f> of 10 kHz.
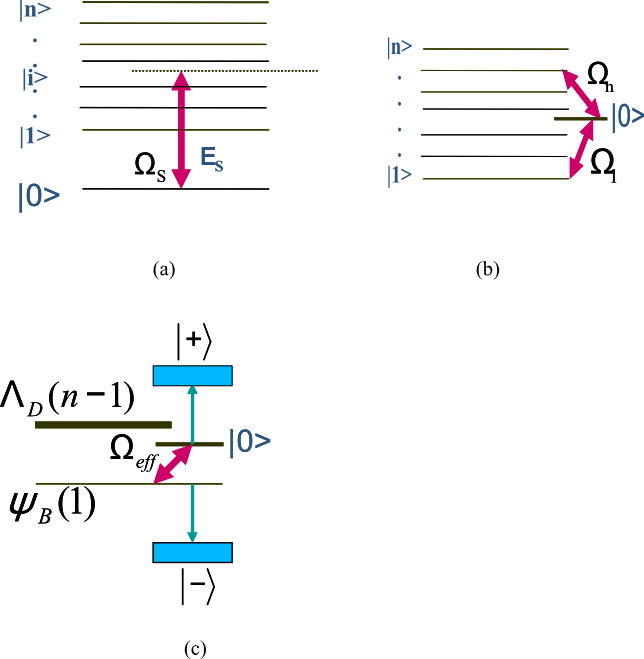
Fig. 9: (a) Coupling scheme of bare states. (b) Coupling diagram in the rotating wave approximation; (c) Coupling of the lower state and the bright state to the dressed states |-> and |+>; dark states from subspace are not involved in coupling.
[1]Harris, S. E., Field, J. E., and Imamoglu, A., Phys. Rev. Lett. 64, 1107 (1990); Harris, S. E., Phys. Today 50, 36 (1997)
[2] Narducci, L. M., Scully, M. O., Oppo, G. -L.,et al., Phys. Rev. A 42, 1630 (1990); Manka, A. S., Doss, H. M., Narducci, L. M., et al., Phys. Rev. A 43, 3748 (1991); Zhou, P., and Swain, S., Phys. Rev. Lett. 77, 3995 (1996)
[3] Kocharovskaya, O., and Khanin, Ya. I., Pi’sma Zh. Eksp. Teor. Fiz. 48, 581(1988) (JETP Lett.48, 630 (1988));Harris, S. E., Phys. Rev. Lett. 62, 1033 (1989)
[4] Fano, U., Phys. Rev. 124 , 1866 (1961)
[5]Alzetta, G., Gozzini, L., Moi, L., and Orriols, G., Il Nuovo Cimento 36B, 5 (1976); Arimondo, E. and Orriols, G., Lettere al Nuovo Cimento 17, 333 (1976)
[6] Taichenachev, A. V., Yudin,V. I., Wynands, R., et al. Phys. Rev. A. 67, 033810 (2003)
[7] Hioe, F.T. and Carroll,C. E., Phys. Rev. A. 37, 3000 (1988)
[8] Zhu, Y., Wang, S., and Mulchan, N. M., Phys. Rev. A. 59, 4005 (1999)
[9] Autler, S. H. and Townes, C. H., Phys. Rev. 100, 703 (1955)
[10] Picque, J. L. and Pinard, J., J. Phys. B: At. Mol. Phys. 9, L77 (1976) ; Delsart, C. and Keller, J.–C., J. Phys. B: At. Mol. Phys. 9, 2769 (1976); Gray, H. R. and Stroud, C. R., Opt. Commun. 25, 359 (1978); Knight, P. L. and Milonni, P. W., Phys. Rep. 66, 21 (1980)
[11] a)Quesada, M. A., Lau, A. M. F., Parker, D. H., and Chandler, D. W., Phys. Rev. A, 36, 4107 (1987); b) Qi, J., Spano, F.C., Kirova, T. et al., Phys. Rev. Lett., 88, 173003 (2002); c) Qi, J. , Lazarov, G., Wang, X., et al., Phys. Rev. Lett., 83, 288 (1999) ; d) Garcia-Fernandez, R., Ekers, A., Klavins, J., et al., Phys. Rev. A, 71, 023401 (2005) ; e) Atherton, P. S., Dalton, B. J., and Dagg, I. R., J. Phys. B: At. Mol. Phys. 19, 277 (1986)
[12] McClean, W. A. And Swain, S., J. Phys. B: At. Mol. Phys. 10, L143 (1977)
[13] Feneuille. S. and Schweighofer, M. -G., J. Physique 36, 781 (1975)
[14]Zare, R. N., 1986, Angular Momentum, (Wiley-Interscience, New York)
[15]Auzinsh, M., Blushs, K., Ferber, R., et al. Opt. Commun. 264, 333 (2006)