The studies of nonlinear mechanics have shown that the so called regime of
dynamic chaos should be considered as typical rather than
exceptional situation [1]. An important example of a physical system
with distinct properties of trajectory instability is a highly
excited hydrogen-like atom in a monochromatic electric microwave
field of frequency
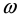 and intensity F [2]. The studies [2] of time evolution of
Rydberg electron (RE) moving in a Coulomb potential in
presence of a microwave field have demonstrated that onset
of the global dynamic chaos in semi-classical trajectories exhibits
a threshold, which depends on the intensityF.
For the given value of n0,
this threshold field Fc
can be found from the relation
and intensity F [2]. The studies [2] of time evolution of
Rydberg electron (RE) moving in a Coulomb potential in
presence of a microwave field have demonstrated that onset
of the global dynamic chaos in semi-classical trajectories exhibits
a threshold, which depends on the intensityF.
For the given value of n0,
this threshold field Fc
can be found from the relation
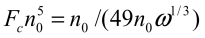 ;
;
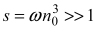 (1)
(1)
If F > Fc, the evolution of the RE acquires the character of the so-called K -systems, i.e., strongly locally unstable Hamiltonian system with intense trajectory mixing in phase space and with rapid uncoupling of correlations between angular dynamic variables [1]. This means that for intensities F above the critical value Fc the motion of the RE in the energy space is unstable (i.e., the separate stochastic layers combine to form the stochastic “sea”) [2]. Or else, for a fixed field intensity F = Fc there exists a well-defined boundary n0 that separates the region n > n0 of chaotic motion from the region n < n0 of regular motion.
In hydrogen-like alkali atoms the field intensity F
relates to the boundary value
 via dipole matrix elements
via dipole matrix elements
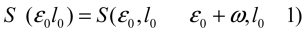 between the Rydberg states
between the Rydberg states
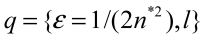 [3]:
[3]:
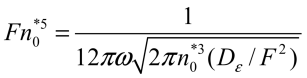 (2)
(2)
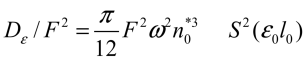 (3)
(3)
The parameter
 plays the role of a diffusion coefficient describing stochastic migration
of the RE through energy levels in the region
plays the role of a diffusion coefficient describing stochastic migration
of the RE through energy levels in the region
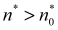 [3]. Due to such migration, the so called RE diffusion ionization in
the microwave field can take place [2].
[3]. Due to such migration, the so called RE diffusion ionization in
the microwave field can take place [2].
A semi-classical approach to the treatment of radiative processes was developed in
[4, 5]. A simple reason for suppression of radiative processes (the
Cooper minimum in atomic photoionization cross sections) was
formulated in terms of classical orbits of RE. It was quantitatively
shown that the values of
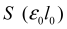 become close to zero provided the difference
become close to zero provided the difference
 between quantum defects has a half-integer value. The latter
corresponds to the situation when a Rydberg l-state
is situated exactly in the middle between two l’-states.
This can be realized in an experiment with Na np-states,
employing the Stark shift of levels by an external electrical field.
This enables blocking the dynamic chaos regime when the l-state
is exactly between two l'-states, since formally
between quantum defects has a half-integer value. The latter
corresponds to the situation when a Rydberg l-state
is situated exactly in the middle between two l’-states.
This can be realized in an experiment with Na np-states,
employing the Stark shift of levels by an external electrical field.
This enables blocking the dynamic chaos regime when the l-state
is exactly between two l'-states, since formally
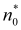 .
In that case the region of global instabilities vanishes and the motion of RE is
regular for all bound levels up to the very ionization continuum.
Tuning the Stark shift away from the two-photon resonance allows one
to vary the diffusion coefficient Dε
and, hence, to tune the threshold
.
In that case the region of global instabilities vanishes and the motion of RE is
regular for all bound levels up to the very ionization continuum.
Tuning the Stark shift away from the two-photon resonance allows one
to vary the diffusion coefficient Dε
and, hence, to tune the threshold
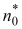 between the zones of chaotic and regular dynamics.
between the zones of chaotic and regular dynamics.