Lifetime and branching ratio measurements using the Autler-Townes effect

We have proposed a novel technique for the determination of lifetimes and branching ratios of excited molecular levels using cw laser excitation (in contrast to the conventional lifetime measurement techniques using excitation by short laser pulses). A system of three rovibrational levels 1, 2 and 3 belonging to different electronic states of the molecules are selectively coupled in a ladder-linkage scheme (Fig. 1). A strong S laser field couples the levels 2 and 3, mixing and modifying them (i.e., creating "dressed states"). This modification is seen in the excitation spectrum as the so-called Autler-Townes doublet (instead of single spectral line observed usually) (Fig. 3),

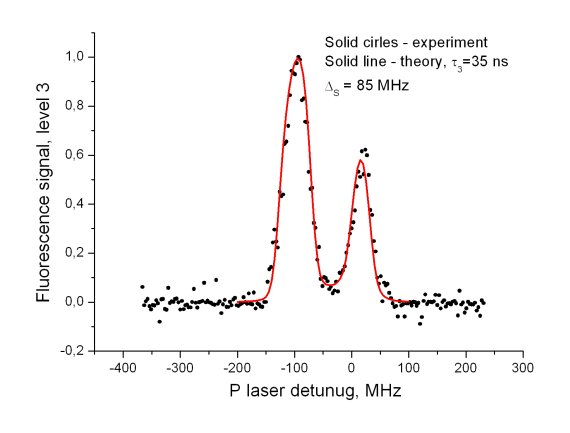
Figure.3.

when the frequency of a weak P laser field is scanned across the resonance between levels 1 and 2. Such experiments can be realised using a setup similar to that shown in Fig. 2, except that P and S laser beams must overlap, and care must be taken to ensure that the diameter of the P laser beam is at least two (but preferably more) times smaller than that of the S laser beam. The Autler-Townes spectra can be used for obtaining the information about excited molecular states in two ways: (i) when the P field intensity is small, the peak ratio in the excitation spectrum of the upper level 3 can be used as a simple and efficient method for the determination of the upper state lifetime; (ii) when the P field intensity is increased, conclusions about branching of the decay of upper electronic state can be drawn from the excitation spectrum of level 2. Both methods can be implemented in the traditional optical double resonance experiments, expanding their potential from mere measurement of energies of rovibrational energy levels to a more complete characterisation of excited molecular states.

Lifetime determination. The method for lifetime determination uses a strong S field and a weak P field. Care must be taken in order to properly take into account line broadening effects. When Doppler broadening is non-negligible, peak areas instead of peak heights must be compared. They can be expressed as [PRA 71, 034401 (2005)] where g2 and g3 are the decay rates of levels 2 and 3, respectively, and q is the mixing angle, which is defined as Obviously, if the detuning of the S laser field DS is chosen large compared to the Rabi frequency WS of the S-field driven transition, then the peak area ratio reduces to the ratio of the decay rates g3 and g2. Hence, if the decay rate of level 2 is known (as is usually the case in double resonance experiments), then the lifetime of the upper level 3 is easily obtained. In the reality, however, the Dopper profile in collimated beams is not exactly described by a Gaussian function, and additional lineshape distortions due to mJ degeneracy of the rotational levels must be taken into account. Therefore more rigorous calculations (like the theoretical curve shown in Fig. 3 obtained by the split propagation technique) may be required [PRA, in preparation]. Nevertheless, in many cases the above equation for the peak ratio can be considered as a good approximation.

Branching ratio determination. The method uses strong S field and strong P field, while the S field frequency is detuned off from resonance with the 2-3 transition. The excitation spectrum of level 2 (Fig. 4)

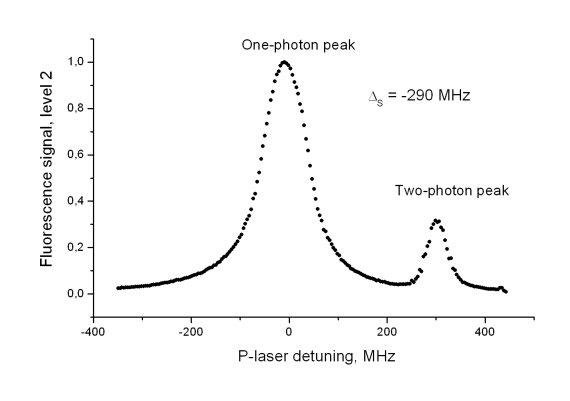
Figure.4.

reveals two peaks: one of them is due to the (saturated) one-photon excitation of level 2 by the P laser field, while the other one is due to cascading to level 2 from level 3, which is excited by two-photon transition with one P photon and one S photon. If it is ensured that two-photon transition pumps all the population through level 3, then the ratio of intensities of two-photon vs one-photon peaks yields the branching coefficient for the decay from level 3 to level 2. If a broadband filter is used as spectral filter, then electronic branching coefficient from the upper electronic state to the intermediate electronic state is obtained. In the analysis, care must be taken to account for finite transit time of molecules through the laser beams. If the lifetime of level 3 is larger than the transit time, then not all the population can be optically pumped through level 3 during the interaction with the laser fields. As a result, the apparent peak ratio in the excitation spectrum of level 2 is not necessarily equal to the branching coefficient. Theoretical analysis of the excitation dynamics using density matrix equations and their solution by Laplace method yielded electronic branching coefficients for the decay from the 5¹Σ_g⁺ and 6¹Σ_g⁺ states to the A¹Σ_u⁺ state of 74% and 95%, respectively.

---

Research activities

• Introduction
• Establishment of the Molecular Beam Laboratory and Laser Centre
• Population transfer to high-lying molecular levels.
• Lifetime and branching ratio measurements using the Autler-Townes effect
• Stochastic phenomena in collisions with Rydberg atoms.
• Stochastic behaviour of photons in absorbing media and its applications.
• Spectroscopic manifestation of radiation trapping in a supersonic beam.
• Ionization of Alkali-Metal Rydberg atoms by blackbody radiation.
• Manipulation of spatial distribution of excited molecules in a beam via dressed-state interference.
• Metastable Rydberg states and blocade effect.
• Stark switching of microwave field induced dynamic chaos regime.
• Line broadening due to optical pumping at unsaturated fields in atomic and molecular beams.
• Lifetime studies of alkali nf-levels.
• Conditions and limitations for resolution of hyperfine structure in the Autler-Townes spectra.
• Fluorescence decay at subnatural times in a magneto optical trap.
• Reconsideration of spectral line profiles affected by transit time broadening
  
• Population switching via interferences in the Autler-Townes effect
• Penning ionization of cold Rb Rydberg atoms due to long-range dipole-dipole interaction