Ionization in cold collisions of Rydberg atoms is possible via two mechanisms: associative and Penning ionization. Associative ionization is a short range process of low efficiency, because it requires close encounters enabling overlap of Rydberg atom wavefunctions (at internuclaer distances R << n*2). In contrast, Penning ionization is a long-range process (at R >> n*2), which is enabled by the dipole-dipole interaction (atomic units are used in this abstract)
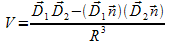(1)
where Di are the dipole moments of both atoms and n denotes the orientation of the internuclear axis.
We consider the formation of atomic ions in an Ager-type processes: one of the Rydbrg atoms undergoes a dipole transition from the initial state nl to a lower state n'l', while the other atom is excited form the initial state nl to the ionization continuum. Such ionization can take place if the energy released in the nl → n'l' transition is equal to (or larger than) the binding energy of electron in the nl state, which is given by the condition n*' < n* sqrt(2) (n* is the effective quantum number). Perturbation theory [1] allows one to express the autoionization width Γ(R) via the photoionization cross section σph of atom in the nl state and the reduced dipole matrix elements |Dnn'| of the nl → n'l' transitions
; 
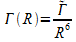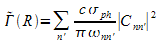(2)
We have evaluated the ionization rates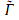 
using semiclassical analytical formulae for both the photoionization cross sections and the dipole matrix elements derived in [2] for alkali atoms. The resulting 
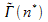is a function that oscillates around the power-law curve 
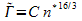with CS = 0.3 and CP = 0.46 for nS and nP states, respectively. These results should help in understanding the ionization dynamics of cold Rydberg gases [3].