When
a Rydberg p-state is situated exactly in the middle of two s-states,
important physical applications of Rydberg atoms in quantum logic
become possible due to realization of the "dipole blockade" [1].
Quantitatively, the double-photon resonance occurs when the
difference
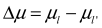between quantum defects of the states involved in the coupling is
equal to ½. We show here that the blockade effect is
accomplished with the suppression of radiative spontaneous processes.
The
reasons for suppressed photoionization were discussed in details by
Seaton [2] (the Cooper minimum in atomic photoionization cross
sections). His arguments about small overlap of wave functions
associated with transitions
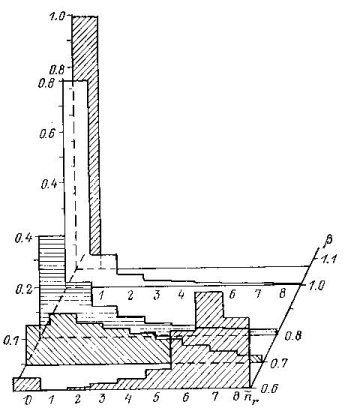
Fig. 1 Natural emission spectra in Sommerfeld atom. Blockade effect is
realized for β = 0.5
are well established: the difference
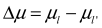must be close to a half-integer value for the optical transition to
be unefficient. The decrease in the efficiency of radiative processes
can be interpreted using classical orbits of Rydberg electrons (RE)
[2]. When a given l-state is very close to the continuum, the
semi-classical treatment yields that the value
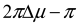is equal to the scattering angle
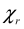of the slow RE by the ionic core. Hence, classical scattering does
not occur when μΔ = 0.5, and, consequently, the probability of
photon absorption is small, and there is no emission. The absence of
classically emitted radiation obviously results in anomalously small
natural linewidths.
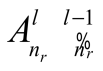with the parameter
,
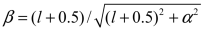which is directly related to the RE scattering angle
,
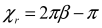is shown in Fig. 1 for the case of a Sommerfeld type model potential
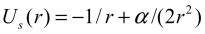[2]. Photons are emitted by the (nr = 8, l = 1) level to a range of
lower levels with radial quantum number
.
The area under curves is normalized to unity. In the vicinity of
,
where p-states are expected to become metastable (
),
the probability distribution of the emission acquires a form
characteristic for black-body radiation, which agrees with the
conceptions of de Broglie [3]